Math Is Fun Forum
You are not logged in.
- Topics: Active | Unanswered
Pages: 1
#1 2010-04-11 20:52:30
- psychist101
- Guest
physics formula, dont understand the maths
hello
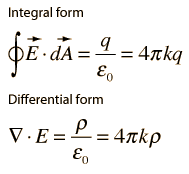
this is gauss law for electricity, but what do all the symbols mean? what i would realy like it an example calculation, so that i can see how exactly it works. i'm more of a physics guy not a maths guy
thx
#2 2010-04-12 19:59:59
- psychist101
- Guest
Re: physics formula, dont understand the maths
bumpp
#3 2010-04-16 10:40:03
- psychist101
- Guest
Re: physics formula, dont understand the maths
????????
#4 2010-04-17 08:28:54
- G_Einstein
- Member

- Registered: 2008-08-30
- Posts: 124
Re: physics formula, dont understand the maths
it is
E is the electric field,which is inependent in this case so
dA=area
if you ahve just one elecric load it is just q
so
If you have a sfear,the area is
so
just
Last edited by G_Einstein (2010-04-17 08:29:39)
Se Zoti vete e tha me goje,se kombet shuhen permbi dhe,por SHqiperia do te roje,per te,per te luftojme ne.
God said that all nation exincts on the ground,but Albania will survive,for it,for it we are fighting.
Offline
#5 2010-04-17 08:35:30
- G_Einstein
- Member

- Registered: 2008-08-30
- Posts: 124
Re: physics formula, dont understand the maths
E is the elctric field,the very elementary piece of the surface that you inegrate,pesilon mean the electric features of the meidum where is the area and q is the electrical load
if you have density you have to make
and to continue.Do you want to make a specifi case ?
For sphere or cilinder with density??
Last edited by G_Einstein (2010-04-17 08:35:51)
Se Zoti vete e tha me goje,se kombet shuhen permbi dhe,por SHqiperia do te roje,per te,per te luftojme ne.
God said that all nation exincts on the ground,but Albania will survive,for it,for it we are fighting.
Offline
#6 2010-04-17 11:07:13
- Identity
- Member

- Registered: 2007-04-18
- Posts: 934
Re: physics formula, dont understand the maths
If you have a closed surface, at each point on the surface you take the dot product of
and and add them up. This will equal the charge contained inside the surface divided by epsilon nought.The symbol
just means a surface integral of a closed surface.In general, for the surface
The surface integral of the vector field
isWhere the RHS is a simple area integral. Note that different orders of the cross product will give different answers. This is because each surface has two orientations (two surface area vectors pointing out from every point on the surface).
This allows you to compute a surface integral.
If you want examples see http://tutorial.math.lamar.edu/Classes/ … grals.aspx
The differential form is derived through an application of Stoke's theorem.
If
This is called the divergence of the vector field.
It's easy enough to compute examples in the differential form.
Last edited by Identity (2010-04-17 11:12:03)
Offline
Pages: 1