Math Is Fun Forum

Jai Ganesh

Administrator

Registered: 2005-06-28

Posts: 48,424

Sagitta (Geometry)

Sagitta (Geometry)

Gist

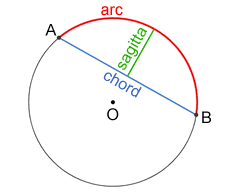
In geometry, the sagitta (sometimes abbreviated as sag) of a circular arc is the distance from the midpoint of the arc to the midpoint of its chord.

The distance from a point in a curve to the chord; also, the versed sine of an arc; so called from its resemblance to an arrow resting on the bow and string.

Details

In geometry, the sagitta (sometimes abbreviated as sag) of a circular arc is the distance from the midpoint of the arc to the midpoint of its chord. It is used extensively in architecture when calculating the arc necessary to span a certain height and distance and also in optics where it is used to find the depth of a spherical mirror or lens. The name comes directly from Latin sagitta, meaning an "arrow".

Formulas

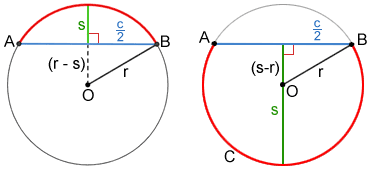
In the following equations, s denotes the sagitta (the depth or height of the arc), r equals the radius of the circle, and l the length of the chord spanning the base of the arc. As

and

are two sides of a right triangle with r as the hypotenuse, the Pythagorean theorem gives us

.

The sagitta may also be calculated from the versine function, for an arc that spans an angle of

, and coincides with the versine for unit circles

.

Approximation

When the sagitta is small in comparison to the radius, it may be approximated by the formula

.

Alternatively, if the sagitta is small and the sagitta, radius, and chord length are known, they may be used to estimate the arc length by the formula

where a is the length of the arc; this formula was known to the Chinese mathematician Shen Kuo, and a more accurate formula also involving the sagitta was developed two centuries later by Guo Shoujing.

.

---

It appears to me that if one wants to make progress in mathematics, one should study the masters and not the pupils. - Niels Henrik Abel.

Nothing is better than reading and gaining more and more knowledge - Stephen William Hawking.