using calculators as proof

mikau · 2009-04-16 13:41:43

so on my last discrete math II class we were given the following question:

for all n ∈ N and x ∈ R, with n < x < n+1, prove that log(x^2) > log(n^2 + n)

I tackled the problem for 20 minutes without success, and then suddenly realized, it was definitely wrong. I grabbed my calculator and chose n = 5, and x = 5.1, and computed:

log(x^2) = log(5.1^2)=3.258...

log(n^2+n) = log(30) = 3.401...

i then wrote 'The claim is false' on the exam sheet, and gave the above calculations to support it, to receive credit for the problem.

After getting the exam back, my teacher laughed at me and said my 'disproof by calculator' was garbage, and reprimanded me for trusting the accuracy of its calculations. He then gave us his own 'proof' of the claim.

but I trusted my calculator more than that, however, i had to play by his rules. So this time i said:
4 < 6 < 9 ⇒ 2 < sqrt(6) < 3

so take n = 2 and x = sqrt(6)

and the claim:
log(x^2) > log(n^2 + n) ⇒ log(6) > log(6) which is obviously false, no calculators needed.

THIS the teacher couldn't ignore, although he was puzzled since he had his own proof of the claim. THEN I discovered and pointed out the error in his proof, which he acknowledged. He gave the whole class full credit for the problem (which was a big deal since not one person managed to do it, and many people did poorly on the test as it was) however he was still puzzled because he was sure this was true by another line of reasoning, and he was so distressed by it that he dismissed the class early.

I don't hold him in contempt for making this mistake, but i do find it surprising that he distrusted the accuracy of a calculator so much, that he didn't even bother to recheck the validity of his claim and instead assumed my calculator was inaccurate to as little as 2 decimal places. In fact, my calculator gives me 9 digits after the decimal place.. why would it bother to give me 9 if the first 2 were not reliable?

so after the test i argued that although calculators may use series approximations, we have methods by which we can determine the error bound, and i am certain our calculators use them to ensure it is accurate to as many digits as are given on the display. He, however, greatly doubted calculators were this sophisticated, and insisted they can never be trusted.

Now i understand that a calculator only gives an approximation, but I at least trust the first n-1 digits if n are given. Is this unreasonable? what do YOU think?

Last edited by mikau (2009-04-16 13:46:19)

bossk171 · 2009-04-16 14:58:07

Not that I'm any kind of expert (I'm certainly not), but it seems really reasonable to me. Hasn't the four color theorem been proved with computers, and isn't the proof generally accepted? Certainly "proof by calculator" isn't unprecedented.

I'm interested to see the "proof" your teacher gave, is it possible to post here?

mikau · 2009-04-16 15:34:48

Sure! Here was his argument:

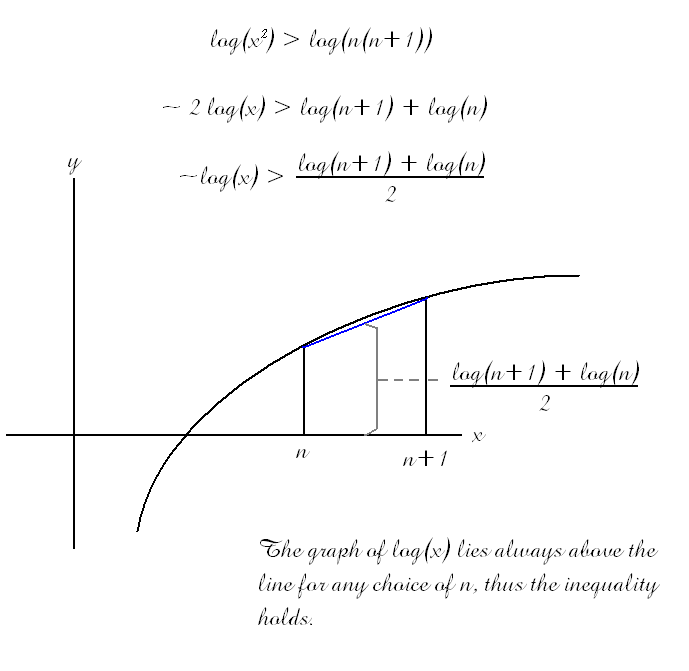
that last sentence is copied directly from his proof. Can you spot the error? Its kind of a fun problem, actually... one of my old calculus teachers used to give 'spot the error' problems, i tend to enjoy them.

JaneFairfax · 2009-04-16 18:54:18

Last edited by JaneFairfax (2009-04-17 01:20:35)

mikau · 2009-04-16 19:35:57

but that maaay be a little harsh, Jane. This is the first time I've EVER caught this particular teacher making a mistake on a proof. He's usually extremely good, which is perhaps why he didn't think to recheck his argument when my calculator disagreed, he's almost always right.

like i said i can forgive him for an honest mistake, i'm just a bit perplexed by what little regard he has for the accuracy of a modern calculator...

(edit) and i don't know why but i'm just loving the font i used in that diagram.. talk about style!

Last edited by mikau (2009-04-16 19:43:04)

bobbym · 2009-04-16 21:46:25

Hi Mikau;

Your counterexample n=5 and x=5.1 should have convinced your teacher that you were right and that there is something wrong with his proof. Unfortunately, he is not wrong about calculators and even frontline computer algebra systems. In some cases they will experience loss of significant digits due to subtractive cancellation and or smearing.

bobbym

Ricky · 2009-04-17 08:17:26

In fact, my calculator gives me 9 digits after the decimal place.. why would it bother to give me 9 if the first 2 were not reliable?

You seem to be under the impression that a calculator understands which decimals are correct and which are not.

Now i understand that a calculator only gives an approximation, but I at least trust the first n-1 digits if n are given. Is this unreasonable? what do YOU think?

Not only is it unreasonable, it is demonstratively false.

Compute:

Noting to follow my order of operations. This should give you 1 over root 2. My calculator gets the 5th digit wrong. Of course, much worse things can happen, and errors lead to more and more errors.

The calculations you are doing are not prone to these sorts of errors since log is a easy to compute and your numbers are not high (or low) enough to lead to them. But you should never trust a calculator to do a mathematicians job.

Ricky · 2009-04-17 08:28:15

Hasn't the four color theorem been proved with computers, and isn't the proof generally accepted? Certainly "proof by calculator" isn't unprecedented.

There is a major difference here. In the proof of the 4-color theorem, we are not talking about decimal representations which always have error. It is possible to make a program that doesn't contain any errors, it is not possible to exactly represent the decimal values 0.1 using a finite number of binary digits. Of course, as a CS professor of mine once said:

"Look engineers. All we're asking for is an infinite number of transistors on a finite-sized chip. You can't even do that?"

mikau · 2009-04-17 17:12:09

You seem to be under the impression that a calculator understands which decimals are correct and which are not.

I am under the impression that there are methods to determine how accurate an approximation (such as a taylor series) is, and how many terms are needed fora given error bound. So if we have a calculator with n digits, take the error bound to be 10^(-n) and add as many as necessary. Do calculators seriously not do this? If not, that's depressing!

In any case, i'd say there's a fundamental difference in the situations here:

in your case, i believe there are 6 operations (square root, multiplication, addition, square root, division) and thus an accumulation of errors.

what I was saying (although i didn't make it precise enough) is if f(x) is a function on the calculator, and you take f(a), (with 'a' a decimal number with n or less digits, n the number of digits on the display) then the result (on a good calculator) should be correct to the first n-1 digits.

I'm not saying that ln(sqrt(2)) is necessarily going to give good results on a 6 digit calculator, but it should give the natural log of '1.41421' (which is not the same thing) correct to 5 decimal places.

In otherwords, I think the calculator accurately calculates f(x), given that x is a quantity that can be completely described with no more than n decimal places. Thus I'd say log(5.1^2) is accurate to at least n-1 decimal places, but log(sqrt(2)) may not be, because we end up taking the log of the approximation of root 2.

Ricky · 2009-04-17 17:41:12

I am under the impression that there are methods to determine how accurate an approximation (such as a taylor series) is, and how many terms are needed fora given error bound. So if we have a calculator with n digits, take the error bound to be 10^(-n) and add as many as necessary. Do calculators seriously not do this? If not, that's depressing!

While we may approximate the error for Taylor series, you are ignoring the fact that what you are computing on can only use a finite number of bits (and typically 32 or 64). And before I go on, calculators use a variety of ways for computing functions, and I don't believe Taylor series is very often involved. The major disadvantage with Taylor series is that it depends upon the point you are calculating the function at, as error accumulates over distance.

The only error you're considering is truncation, which is not the only type of error that occurs. For example, take your function on your calculator to be e^x. Obviously for relatively small number sizes you get simply run out of bits and get overflow error. With the advanced definitions of floating numbers that are in use today this doesn't quite happen, but what does happen is that numerical results become less and less accurate the higher the number.

Seeing what exactly occurs is a bit complex, because we don't exactly do floating-point computations in a straightforward way. But it's just a question of information: you have 32 (or 64) bits, you obviously can't represent every number between -1.000.000.000.000 and 1.000.000.000.000 with up to 9 decimal digits. You would need to be able to represent 10^(12+9) numbers using only 64-bits which have 18.446.744.073.709.551.616 unique values. A little application of the pigeon-hole principle shows this is indeed impossible.

in your case, i believe there are 6 operations (square root, multiplication, addition, square root, division) and thus an accumulation of errors.

Actually, the only significant error that occurs in the above is when I add 1 to a really really big number. All the other operations (I believe, but would need to double check) are fairly safe... numerically.

bobbym · 2009-04-18 04:02:03

Hi Mikau;

Typically they haven't used taylor series for a long time. They were replaced by Pade approximants and economized polynomials. These provide better accuracy over a wider range than a Taylor series. A human thinks of the number line as having all the real numbers but to a computer there are lots of missing numbers on it. Simply, because many numbers are not expressible in binary on a finite machine. Like 1/3,1/6,1/9... for instance.

bobbym

Math Is Fun Forum

#1 2009-04-16 13:41:43

using calculators as proof

#2 2009-04-16 14:58:07

Re: using calculators as proof

#3 2009-04-16 15:34:48

Re: using calculators as proof

#4 2009-04-16 18:54:18

Re: using calculators as proof

#5 2009-04-16 19:35:57

Re: using calculators as proof

#6 2009-04-16 21:46:25

Re: using calculators as proof

#7 2009-04-17 08:17:26

Re: using calculators as proof

#8 2009-04-17 08:28:15

Re: using calculators as proof

#9 2009-04-17 17:12:09

Re: using calculators as proof

#10 2009-04-17 17:41:12

Re: using calculators as proof

#11 2009-04-18 04:02:03

Re: using calculators as proof

Board footer