crème de la crème

Jai Ganesh · 2015-10-25 12:27:50

(1) The term "Golden Rule", or "Golden law" began to be used widely in the early 17th century in Britain; the earliest known usage is that of Charles Gibbon in 1604.

Antiquity

Ancient Egypt

Possibly the earliest affirmation of reciprocity reflecting the Ancient Egyptian concept of Maat appears in the story of The Eloquent Peasant, which dates to the Middle Kingdom (c. 2040 – c. 1650 BC): "Now this is the command: Do to the doer to make him do." This proverb embodies the du ut des principle. A Late Period (c. 664 BC – 323 BC) papyrus contains an early negative affirmation of the Golden Rule: "That which you hate to be done to you, do not do to another."

Ancient Near East

The earliest known text of the positive form of the Golden Rule is the following Biblical verse (538–332 BCE): "You shall not take vengeance or bear a grudge against your kinsfolk. Love your neighbor as yourself: I am the LORD." (Leviticus 19:18)

Ancient China

The Golden Rule existed among all the major philosophical schools of Ancient China: Mohism, Taoism, and Confucianism. Examples of the concept include:

"Never impose on others what you would not choose for yourself." — Confucius (c. 500 BC)
"If people regarded other people's families in the same way that they regard their own, who then would incite their own family to attack that of another? For one would do for others as one would do for oneself." — Mozi (c. 400 BC)
"Regard your neighbor's gain as your own gain, and your neighbor's loss as your own loss." — Laozi (c. 500 BC)

Ancient India

Sanskrit tradition

In Mahābhārata, the ancient epic of India, (c 800-700 BC) comes a discourse where the wise minister Vidura advises the King Yuddhiśhṭhira thus, "Listening to wise scriptures, austerity, sacrifice, respectful faith, social welfare, forgiveness, purity of intent, compassion, truth and self-control — are the ten wealth of character (self). O king aim for these, may you be steadfast in these qualities. These are the basis of prosperity and rightful living. These are highest attainable things. All worlds are balanced on dharma, dharma encompasses ways to prosperity as well. O King, dharma is the best quality to have, wealth the medium and desire (kāma) the lowest. Hence, (keeping these in mind), by self-control and by making dharma (right conduct) your main focus, treat others as you treat yourself."

Tamil tradition

In the Section on Virtue, and Chapter 32 of the Tirukkuṛaḷ (c. 200 BC – c. 500 AD), Tiruvalluvar says: Why does a man inflict upon other creatures those sufferings, which he has found by experience are sufferings to himself ? (K. 318) Let not a man consent to do those things to another which, he knows, will cause sorrow. (K. 316) He furthermore opined that it is the determination of the spotless (virtuous) not to do evil, even in return, to those who have cherished enmity and done them evil. (K. 312) The (proper) punishment to those who have done evil (to you), is to put them to shame by showing them kindness, in return and to forget both the evil and the good done on both sides. (K. 314)

Ancient Greece

The Golden Rule in its prohibitive (negative) form was a common principle in ancient Greek philosophy. Examples of the general concept include:

"Avoid doing what you would blame others for doing." – Thales (c. 624 BC – c. 546 BC)
"What you do not want to happen to you, do not do it yourself either. " – Sextus the Pythagorean. The oldest extant reference to Sextus is by Origen in the third century of the common era.
"Do not do to others that which angers you when they do it to you." – Isocrates(436–338 BC)

Ancient Persia

The Pahlavi Texts of Zoroastrianism (c 300 BC-1000 AD) were an early source for the Golden Rule: "That nature alone is good which refrains from doing to another whatsoever is not good for itself." Dadisten-I-dinik, 94,5, and "Whatever is disagreeable to yourself do not do unto others." Shayast-na-Shayast 13:29

bobbym · 2015-10-25 17:58:53

Hi;

Very good!

Jai Ganesh · 2015-10-25 20:19:32

Hi bobbym,

Thanks!

Jai Ganesh · 2015-10-27 09:16:16

A Magnificent Mathematician and an Astonishing Astronomer!

(2) Robert Recorde

Throughout their education, students will come across the most ubiquitous symbol in all of mathematics. It’s the symbol that defines all equations. It is the equal sign. But where did it come from?

Robert Recorde (ca. 1512-1558) was a Welsh physician and mathematician. At the age of fifteen, he entered Oxford University, graduating in 1531. In the same year he was elected a Fellow of All Souls College. Moving to Cambridge University he obtained a degree in medicine in 1545. He is known as the founder of the English School of Mathematics and was the first person to write mathematical books in English. He also introduced, among other things, the idea of placing two hyphens in parallel to symbolize the balance of two expressions in a mathematical equation.

He wrote a math textbook with a most convoluted title: “The Whetstone of Witte, whiche is the seconde parte of Arithmeteke: containing the extraction of rootes; the cossike practise, with the rule of equation; and the workes of Surde Nombers” (Published in 1557 Y) (Robert Recorde's The Whetstone of Witte is published, the first English book on algebra, containing the first recorded use of the equals sign and also the first use in English of plus and minus signs.) The book covers topics including whole numbers, the extraction of roots and irrational numbers as well as the execution of arithmetic operations.

This is the page in which he defines the familiar symbol:

“And to avoide the tedious repetition of these woordes: is equalle to: I will sette as I doe often in woorke use, a paire of paralleles, or gemowe lines of one length, thus: =, because noe. 2. thynges, can be moare equalle.”

He uses this symbol to subsequently express numerous equations, beginning at the bottom of this page. Thus, it can be said that the first math equation to be expressed using this modern notation is 14x + 15 = 71. Thankfully, by the time this symbol was consistently used in the 1700s, the two parallel lines (as well as other symbols he defined) were made more compact.

Robert Recorde is honored with a wall tablet at St. Mary’s Church. It is located in his birth town of Tenby, Pembrokeshire, Wales. It documents his achievements to mathematics:

“To his genius we owe the earliest important English treatises on algebra, arithmetic, astronomy, and geometry: He also invented the sign of equality, =, now universally adopted by the civilized world.”

There is also a display at the Tenby Museum & Art Gallery documenting the achievements of this Welsh mathematical pioneer.

(3) The French astronomer Charles Messier was born in Lorraine on June 26, 1730. When he was 11 his father died and being the tenth of twelve children Messier consequently had little opportunity for education. As a boy he developed an avid interest in astronomy after seeing the brilliant six-tailed comet of 1744. Even though Messier came from a poor family and had limited schooling he was hired at the age of 21 as a draftsman by Joseph-Nicholas de l'Isle, Astronomer to the French Navy. Messier soon learned to use astronomical instruments and became a skilled observer. He was promoted to clerk at the Marine Observatory at the Hotel de Cluny in Paris by the mid-1750's.

Edmund Halley had predicted that the comet of 1682 would return in late 1758 or early 1759. Using charts that de l'Isle had incorrectly prepared, Messier began searching for the comet with a small reflector. On January 21, 1759 he located the comet but de l'Isle initially refused to let Messier announce his discovery. (As fate would have it the comet was first sighted on Christmas Night of 1758 by a German farmer and amateur astronomer named Palitzch.) Undaunted by the embarrassment of the late announcement, Messier from that time onward devoted himself to searching for comets. In the coming years he held a near monopoly on comet discoveries claiming to have found 21 by 1798.

Charles Messier used over a dozen telescopes during his career but his favorite was a 7.5 inch 104x Gregorian reflector. Later when the apochromatic refractor became available he utilized several 3.5 inch 120x apochromatics.

On August 28, 1758 Messier found by chance a small nebulous (cloudy) object in the constellation of Taurus while observing a comet he had discovered two weeks earlier. This object, a supernova remnant known today as the Crab Nebula (M1), was later to become the first entry on a list of comet-like objects that eventually became the most famous catalog of galaxies, nebulae and star clusters in astronomy. Ironically, Messier became famous historically for his catalog of time-wasting "objects to avoid" when comet hunting and not for the comets he discovered.

Messier became the chief astronomer of the Marine Observatory in 1759. He was elected to the Royal Society of London in 1764 and the Paris Academy of Sciences in 1770.

During a seven-month period of searching for comets in 1764 Messier added 38 objects to his list including M13 (the great globular cluster in Hercules), the Swan nebula (M17) in Sagittarius and the Andromeda galaxy (M31). In January of the following year he logged M41, the open cluster southwest of Sirius. Messier determined the positions of the Orion Nebula (M42 and M43), the Beehive cluster (M44) and the Pleiades (M45) on March 4, 1769.

Messier also began compiling reports of discoveries by other astronomers. In fact, only 17 of the 45 objects in the first installment of Messier's catalog published in 1774 were discovered by Messier himself. (The first object that Messier is given credit for discovering is the globular cluster M3 which was first located on May 3, 1764.) By 1780 the number of objects in his catalog had increased to 80.

Because of Messier's undeniable success as a comet hunter King Louis XV of France nicknamed him the "Ferret of Comets". But Messier was no mathematician and relied on his aristocratic friend Bouchart de Saron who was the President of the French Assembly to compute the orbits of his comets. Messier also collaborated with the younger astronomer Pierre Francois Andre Mechain who was a successful comet hunter as well. During 1780 and 1781 he discovered some 32 new nebulous objects and reported their positions to Messier. Mechain was the first astronomer to note the profusion of nebulae in Coma Berenices and Virgo. Messier recorded 9 new nebulae in this region in a single night on March 18, 1781.

On April 13, 1781 Messier added the one hundredth object to the catalog. Three subsequent observations by Mechain were included hastily without verification and what was to be the final revision of the catalog was published in 1781. Forty of the 103 objects listed had been discovered by Messier and 27 by Mechain. In November of 1781 Messier suffered a severe fall and further work on his catalog was ended.

During his convalescence Messier was provided for by President de Saron and members of the Academie Royale. After a year of recuperating Messier made preparations to study the transit of Mercury and began observing the newly discovered planet Uranus as well as searching for more comets.

The French Revolution was a disastrous period for Messier and his compatriots. In 1794 Messier lost his Academie pension and naval salary and the navy stopped paying the rent on his observatory. President de Saron, the talented mathematician who was one of the first men to realize that William Herschel's Uranus was in fact a planet, was guillotined a few days after computing the orbit of a comet that Messier had discovered the previous year. Mechain lost his estate and all of his savings. With the coming of Napoleon Bonaparte the lives of Messier and Mechain improved greatly. Mechain was made the director of the Paris Observatory and both he and Messier were admitted to the new Academy of Sciences and the Bureau of Longitudes. Messier received the cross of the Legion of Honor from Napoleon himself.

Messier made his last discovery in 1798. He continued to observe until he suffered a debilitating stroke. Two years later on April 12, 1817 he died at the age of 86.

In the twentieth century 7 objects known to have been logged by Messier were added to the Messier Catalog. M110, the final entry, was added in 1967.

Today it is known that M40 is merely a binary star and M73 is only an asterism. M102 is thought to be a duplication of M101 but NGC 5866 is often accepted as being M102. The true identity of M91 is also questionable. Because of an error in their coordinates M47 and M48 were at one time deemed to be "lost" Messier objects.

Charles Messier was limited as a scientist but he was an astute observational astronomer who studied sunspots, eclipses and occultations in addition to discovering many comets and nebulous objects. He was so totally dedicated to astronomy that when his wife lay dying it was with the greatest reluctance that he left his telescope to be at her side. Messier's lasting legacy to amateur astronomy, the Messier Catalog, includes most of the best deep sky objects visible in the northern hemisphere.

Last edited by Jai Ganesh (2015-10-27 09:56:26)

Jai Ganesh · 2015-11-02 16:50:23

(4) Judit Polgár (born 23 July 1976) is a Hungarian chess grandmaster. She is generally considered the strongest female chess player in history. In 1991, Polgár achieved the title of Grandmaster at the age of 15 years and 4 months, at the time the youngest to have done so, breaking the record previously held by former World Champion Bobby Fischer. She is the youngest ever player, to date, to break into the FIDE Top 100 players rating list, being ranked No. 55 in the January 1989 rating list, at the age of 12. She is the only woman to qualify for a World Championship tournament, having done so in 2005. She is the first, and to date, only woman to have surpassed the 2700 Elo rating barrier, reaching a career peak rating of 2735 and peak world ranking of #8, both achieved in 2005. She was the number 1 rated woman in the world from January 1989 up until the March 2015 rating list, when she was overtaken by Chinese player Hou Yifan; she was the No. 1 again in the August 2015 women's rating list, in her last appearance in the FIDE World Rankings.

She has won or shared first in the chess tournaments of Hastings 1993, Madrid 1994, León 1996, U.S. Open 1998, Hoogeveen 1999, Sigeman & Co 2000, Japfa 2000, and the Najdorf Memorial 2000.

Polgár is the only woman to have won a game from a reigning world number one player, and has defeated eleven current or former world champions in either rapid or classical chess: Magnus Carlsen, Anatoly Karpov, Garry Kasparov, Vladimir Kramnik, Boris Spassky, Vasily Smyslov, Veselin Topalov, Viswanathan Anand, Ruslan Ponomariov, Alexander Khalifman, and Rustam Kasimdzhanov.

On 13 August 2014, she announced her retirement from competitive chess. In June 2015, Polgar was elected as the new captain and head coach of the Hungarian national men's team. On 20 August 2015, she received Hungary's highest decoration, the Grand Cross of the Order of Saint Stephen of Hungary.

bobbym · 2015-11-03 02:52:29

Hi;

There are 3 of them, 3 sisters. They are all unusually strong chess players. Judit, possibly can associate her playing ability with playing lots of speed chess with the great Robert "Bobby" Fischer whom it was rumored stayed at their house during his long escape from reality.

Agnishom · 2015-11-03 04:41:58

What is this thread about?

bobbym · 2015-11-03 06:23:50

The title means cream of the cream. Translates into the best of the best.

Jai Ganesh · 2015-11-03 08:29:28

The three sisters "

Jai Ganesh · 2015-11-03 17:40:14

Two men, both seriously ill, occupied the same hospital room. One man was allowed to sit up in his bed for an hour each afternoon to help drain the fluid from his lungs. His bed was next to the room's only window. The other man had to spend all his time flat on his back.The men talked for hours on end. They spoke of their wives and families, their homes, their jobs, their involvement in the military service, where they had been on vocation.
Every afternoon when the man in the bed by the window could sit up, he would pass the time by describing to his roommate all the things he could see outside the window. The man in the other bed began to live, for those one-hour periods where his world would be broadened and enlivened by all the activity and color of the world outside. The window overlooked a park with a lovely lake. Ducks and swans played on the water while children sailed their model boats. Young lovers walked arm-in-arm amidst flowers of every color of the rainbow. Grand old trees graced the landscape, and a fine view of the city skyline could be seen in the distance. As the man by the window described all this in exquisite detail, the man on the other side of the room would close his eyes and imagine the picturesque scene. One warm afternoon the man by the window described a parade passing by. Although the other man couldn't hear the band - he could see it in his mind's eye as the gentleman by the window portrayed it with descriptive words. Days and weeks passed. One morning, the day nurse arrived to bring water for their baths only to find the lifeless body of the man by the window, who had died peacefully in his sleep. She was saddened and called the hospital attendants to take the body away. As soon as it seemed appropriate, the other man asked if he could be moved next to the window. The nurse was happy to make the switch, and after making sure he was comfortable, she left him
alone. Slowly, painfully, he propped himself up on one elbow to take his first look at the world outside. Finally, he would have the joy of seeing it for himself. He strained to slowly turn to look out the window beside the bed. It faced a blank wall. The man asked the nurse what could have compelled his deceased roommate having had described such wonderful things outside this window.The nurse responded that the man was blind and could not even see the wall. She said, "Perhaps he just wanted to encourage you."
Epilogue: There is tremendous happiness in making others happy, despite our own situations. Shared grief is half the sorrow, but happiness when shared, is doubled. If you want to feel rich, just count all
the things you have that money can't buy.

"Today is a gift, that's why it is called the present."

Last edited by Jai Ganesh (2016-02-28 00:48:41)

Jai Ganesh · 2015-11-04 01:55:41

What is a Fermi Question?

A Fermi question requires estimation of physical quantities to arrive at an answer. Throughout his work, Fermi was legendary for being able to figure out things in his head, using information that initially seems to meager for a quantitative result. He used a process of "zeroing in" on problems by saying that the value in question was certainly larger than one number and less than some other amount. He would proceed through a problem in that fashion and, in the end, have a quantified answer within identified limits.

In a Fermi question, the goal is to get an answer to an order of magnitude (typically a power of ten) by making reasonable assumptions about the situation, not necessarily relying upon definite knowledge for an
"exact" answer.

A Fermi question is posed with limited information given.

How many water balloons would it take to fill the school gymnasium?
How many piano tuners are there in New York City?
What is the mass in kilograms of the student body in your school?
A Fermi question requires that students ask many more questions.
How big is a water balloon?
What are the approximate dimensions of the gym?
What measurment must be estimated using the dimensions of the gym?
... and the list goes on.
A Fermi question demands communication.
A Fermi question utilizes estimation.
A Fermi question emphasizes process rather than "the" answer.

Example 1:
How Many Piano Tuners Are In New York City?
How might one figure out such a thing?? Surely the number of piano tuners in some way depends on the
number of pianos. The number of pianos must connect in some way to the number of people in the area.
Approximately how many people are in New York City?
10,000,000

Does every individual own a piano?
No

Would it be reasonable to assert that "individuals don't tend to own pianos; families do?
Yes.

About how many families are there in a city of 10 million people?
Perhaps there are 2,000,000 families in NYC.

Does every family own a piano?
No.
Perhaps one out of every five does.
That would mean there are about 400,000 pianos in NYC.

How many piano tuners are needed for 400,000 pianos?
Some people never get around to tuning their piano; some people tune their piano every month. If we assume
that "on the average" every piano gets tuned once a year, then there are 400,000 "piano tunings" every year.

How many piano tunings can one piano tuner do?
Let's assume that the average piano tuner can tune four pianos a day. Also assume that there are 200
working days per year. That means that every tuner can tune about 800 pianos per year.

How many piano tuners are needed in NYC?
The number of tuners is approximately 400,000/800 or 500 piano tuners.

Try it yourself.
Use different assumptions for various factors. It is unlikely that you can justify an answer greater than a
factor of 10 or smaller than a factor of 10 from the number originally obtained; that is to say, there are
probably not more than 5000 tuners and surely no less than 50. Thus the answer obtained is good to within an
"order of magnitude".

Example 2:
How Many Jelly Beans Fill A One-Liter Bottle?
As with any Fermi question, there are multiple directions from which the problem can be approached.
Solution 1 illustrates a more algorithmic approach;
solution 2 is more intuitive. In both solutions, it is understood that one liter is equal to 1000 cubic
centimeters.

Solution 1
What is the approximate size a jelly bean?
An examination of a jelly bean reveals that is approximately the size of a small cylinder that measures about 2 cm long by about 1.5 cm in diameter.

Do jelly beans "completely fill the liter bottle"?
The irregular shape of jelly beans result in them not being tightly packet; approximately 80% of the volume
of the bottle is filled. The number of jelly beans is the occupied volume of the jar divided by the volume of a single jelly bean
Number of beans = (Occupied Volume of Jar)/(Volume of 1 Bean)

The volume of one jelly bean is approximated by the volume of a small cylincer 2 cm long and 1.5 cm in
diameter
Volume of 1 Jelly Bean = h(pi)(d/2)^2 = 2cm x 3
(1.5cm/2)^2 = 27/8 cubic centimers
Thus the approximate number of beans in the jar is
Number of beans = (.80 x 1000 cubic centimeters)/(27/8 cubic centimeters) = approx 240 jelly beans

Have your students try it out with jelly beans and a liter bottle or jar. If you don't have a liter jar, use a quart jar (.95 liter)

Solution 2
Have your students construct or visualize a paper cube that measures 1 cubic inch.
How many jelly beans will fit in the cube?
Approximately 4

How many cubic inches are there in 1 liter?
1 inch = approx 2.54 centimeters. Therefore 1 cubic inch = approx. 16 cubic centimeters
1000 cubic centimeters/16 cubic centimeters = approx 62 cubic inches in one liter.

How many jelly beans are there in the one liter container?

62 x 4 = approximately 248 jellybeans

Agnishom · 2015-11-04 04:15:44

bobbym wrote:

The title means cream of the cream. Translates into the best of the best.

What do I need to accomplish to make it to this list?

Jai Ganesh · 2015-11-05 11:42:23

The number e is an important mathematical constant that is the base of the natural logarithm. It is approximately equal to 2.71828, and is the limit of

as n approaches infinity, an expression that arises in the study of compound interest. It can also be calculated as the sum of the infinite series.

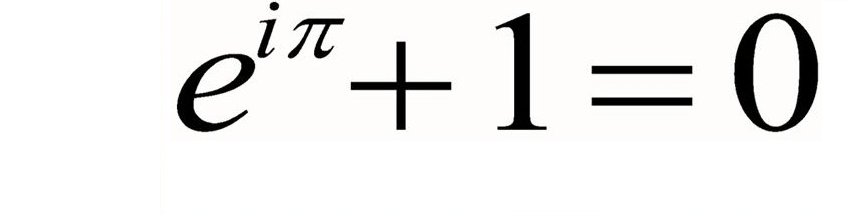
The constant can be defined in many ways. For example, e can be defined as the unique positive number a such that the graph of the function

has unit slope at x = 0. The function is called the exponential function, and its inverse is the natural logarithm, or logarithm to base e. The natural logarithm of a positive number k can also be defined directly as the area under the curve y = 1/x between x = 1 and x = k, in which case e is the number whose natural logarithm is 1. There are alternative characterizations.

Sometimes called Euler's number after the Swiss mathematician Leonhard Euler, e is not to be confused with γ, the Euler–Mascheroni constant, sometimes called simply Euler's constant. The number e is also known as Napier's constant, but Euler's choice of the symbol e is said to have been retained in his honor. The constant was discovered by the Swiss mathematician Jacob Bernoulli while studying compound interest.

The number e is of eminent importance in mathematics, alongside

. All five of these numbers play important and recurring roles across mathematics, and are the five constants appearing in one formulation of Euler's identity. Like the constant π, e is irrational: it is not a ratio of integers. Also like π, e is transcendental: it is not a root of any non-zero polynomial with rational coefficients. The numerical value of e truncated to 50 decimal places is

2.71828182845904523536028747135266249775724709369995..

History

The first references to the constant were published in 1618 in the table of an appendix of a work on logarithms by John Napier. However, this did not contain the constant itself, but simply a list of logarithms calculated from the constant. It is assumed that the table was written by William Oughtred. The discovery of the constant itself is credited to Jacob Bernoulli, who attempted to find the value of the following expression (which is in fact e):

.

The first known use of the constant, represented by the letter b, was in correspondence from Gottfried Leibniz to Christiaan Huygens in 1690 and 1691. Leonhard Euler introduced the letter e as the base for natural logarithms, writing in a letter to Christian Goldbach of 25 November 1731. Euler started to use the letter e for the constant in 1727 or 1728, in an unpublished paper on explosive forces in cannons,[11] and the first appearance of e in a publication was Euler's Mechanica (1736). While in the subsequent years some researchers used the letter c, e was more common and eventually became the standard.

Asymptotics

The number e occurs naturally in connection with many problems involving asymptotics. A prominent example is Stirling's formula for the asymptotics of the factorial function, in which both the numbers e and pi enter:

.

A particular consequence of this is

.

Jai Ganesh · 2015-11-05 14:56:22

The term was invented by Milton Sirotta, the 9-year nephew of mathematician Edward Kasner, who had asked his nephew what he thought such a large number should be called. Such a number, Milton apparently replied after a short thought, could only be called something as silly as a "googol."

Later, another mathematician devised the term googolplex for 10 to the power of googol - that is, 1 followed by 10 to the power of 100 zeros. Frank Pilhofer has determined that, given Moore's Law (which is that computer processor power doubles about every 1 to 2 years), it would make no sense to try to print out a googolplex for another 524 years - since all earlier attempts to print a googolplex out would be overtaken by the faster processor.

Larry Page and Sergey Brin, the founders of Google, named their search engine after the term googol. In 1997, Larry was brainstorming names with other Stanford graduate students, including Sean Anderson, and looking at available domain names. Anderson miskeyed googol as "google" and found it available. Larry liked it and the name "Google" stuck. Google's corporate headquarters is called the GooglePlex, an affectionately tongue-in-cheek reference to the origins of the company name.

Jai Ganesh · 2015-11-07 00:19:20

Stefanie Maria Graf (born 14 June 1969) is a German former world No. 1 tennis player.

Graf won 22 Grand Slam singles titles. Her 22 singles titles is second all-time behind Margaret Court (24), and marks the record for most Major wins by a tennis player (male or female) since the introduction of the Open Era in 1968. In 1988, she became the first and only tennis player (male or female) to achieve the Golden Slam by winning all four Grand Slam singles titles and the Olympic gold medal in the same calendar year, furthermore, she is the only tennis player to have won each Grand Slam event at least 4 times.

Graf was ranked World No. 1 by the Women's Tennis Association (WTA) for a record 377 total weeks—the longest period for which any player, male or female, has held the number-one ranking since the WTA and the Association of Tennis Professionals began issuing rankings. She won 107 singles titles, which ranks her third on the WTA's all-time list after Martina Navratilova (167 titles) and Chris Evert (157 titles). She and Margaret Court are the only players, male or female, to win 3 grand slams in a calendar year 5 times (1988, 1989, 1993, 1995 and 1996).

A notable feature of Graf's game was her versatility across all playing surfaces, having won each of the four Majors at least four times, the only player to do so, and she is best known for her great footwork and for her powerful forehand drive. Graf won six French Open singles titles (second to Evert), seven Wimbledon singles titles, and five U.S. Open singles titles. She is the only singles player (male or female) to have achieved a Grand Slam since hard court was introduced as a surface at the US Open in 1978. Consequently, Graf's Grand Slam was achieved on grass, clay, and hard court while the previous five Grand Slams were decided on only grass and clay. Graf reached thirteen consecutive Grand Slam singles finals, from the 1987 French Open through to the 1990 French Open, winning nine of them. She won 5 consecutive Majors (1988 Australian Open to 1989 Australian Open), and 7 Majors out of 8, in 2 calendar years (1988 Australian Open to 1989 US Open, except 1989 French Open). She reached a total of 31 Grand Slam singles finals.

Graf is regarded by some to be the greatest female tennis player of all time. Navratilova included Graf on her list of great players. In 1999 Billie Jean King said "Steffi is definitely the greatest women's tennis player of all time". In December 1999, Graf was named the greatest female tennis player of the 20th century by a panel of experts assembled by the Associated Press. Tennis writer Steve Flink, in his book The Greatest Tennis Matches of the Twentieth Century, named her as the best female player of the 20th century. In March 2012, Tennis Channel picked Graf as the greatest female tennis player ever in their list of 100 greatest tennis players of all time.

Graf retired in 1999 while she was ranked World No. 3. She married former World No. 1 men's tennis player Andre Agassi in October 2001. The couple have two children – Jaden Gil and Jaz Elle. Graf was inducted into the Tennis Hall of Fame in 2004.

Jai Ganesh · 2015-11-07 12:43:37

10.

You might have heard the expression “it’s a figure of speech,” but what does that really mean? A figure of speech is just that – figurative language. It might be words with a literal meaning, a certain arrangements of words, or a phrase with a meaning that is something entirely other than that of the words themselves. Figures of speech can be refreshing and fun, but for some – especially those who are not native English speakers – a figure of speech can be very confusing. Here are some of the most common figures of speech and what they mean.

List of Figure of Speech and Examples

1. Alliteration

This is a very common figure of speech that involves using words that begin with the same sound.

For instance, “Sally sells sea shells by the seashore” is alliteration – and try saying it fast to see how difficult it is! It is often used in advertising slogans to create something catchy that more people will remember.

2. Anaphora

This figure of speech uses a specific clause at the beginning of each sentence or point to make a statement.

For instance: “Good night and good luck” is an example of the beginning word being the same. The more it is used, the more of an emotional effect is can evoke among those who are listening. Another example is "Mad world! Mad kings! Mad composition!" from King John, II, I by William Shakespeare.

3. Assonance

Remember the phrase “I Like Ike”? It was a very common phase for those who supported Dwight Eisenhower during his presidential run. This is a figure of speech that focuses on the vowel sounds in a phrase, repeating them over and over to great effect.

4. Hyperbole

“It was as big as a mountain! It was faster than a cheetah! It was dumber than a rock!” This figure of speech makes things seem much bigger than they really were by using grandiose depictions of everyday things. Hyperbole is often seen as an exaggeration that adds a bit of humor to a story.

5. Irony

This figure of speech tries to use a word in a literal sense that debunks what has just been said. “Gentlemen, you can’t fight in here! This is the War Room!” from Dr. Strangelove is a great example. It is often used to poke fun at a situation that everyone else sees as a very serious matter.

There are different types of irony and here are the details and examples.

6. Metaphor

The use of metaphor compares two things that are not alike and finds something about them to make them alike.

“My heart is a lonely hunter that hunts on a lonely hill” from a book by William Sharp is a good example of metaphor. Some writers try to use this style to create something profound out of comparing two things that appear to have nothing at all in common.

7. Simile

In this figure of speech, two things are compared that are not really the same, but are used to make a point about each other.

“Life is like a box of chocolates; you never know what you’re going to get” is a famous line from the movie Forrest Gump that illustrates the simile. This is often used to make an emotional point about something. The difference between simile and metaphor is that you can obviously see words "like" in the sentence.

8. Metonymy

In this figure of speech, one word that has a very similar meaning can be used for another. Using the word “crown” for “royalty” or “lab coats” for “scientists” are two examples. In some ways it can be seen as a nickname for something else; for instance, “The White House said” doesn’t actually mean the White House said it (a house can’t speak!) but that the President said it. However, we all understand the meaning, and so the words are interchangeable.

9. Onomatopoeia

This is the use of a word that actually sounds like what it means. Good examples include “hiss” or “ding-dong” or “fizz.” These words are meant to describe something that actually sounds very much like the word itself. This is a trick often used in advertising to help convey what something is really like.

10. Paradox

This figure of speech completely contradicts itself in the same sentence. Famous quotes that illustrate this from George Orwell’s “1984” include: “War is peace. Ignorance is strength. Freedom is slavery.” Though we know these things aren’t true, they present an interesting paradox that makes a person think seriously about what they have just read or heard.

11. Personification

This is a way of giving an inanimate object the qualities of a living thing. “The tree quaked with fear as the wind approached” is an example; “The sun smiled down on her” is another. This can sometimes be used to invoke an emotional response to something by making it more personable, friendly and relatable.

12. Pun

This play on words uses different senses of the word, or different sounds that make up the word, to create something fun and interesting. For instance: “I would like to go to Holland some day. Wooden shoe?” is a pun that actually means “wouldn’t you?” Sometimes puns are so subtle that they can be tough to pick up unless you are really listening for them.

13. Synecdoche

This is a figure of speech in which one thing is meant to represent the whole. A few good examples include “ABCs” for alphabet, “new set of wheels” for car, or “9/11” to demonstrate the whole of the tragedy that happened in the United States on September 11, 2001. This is often used in journalism as a type of shorthand.

14. Understatement

This is a situation in which the thing discussed is made to seem much less important than it really is. This famous line from Catcher in the Rye is a good example: “I have to have this operation. It isn’t very serious. I have this tiny tumor on the brain.” Understatement can often be used to comedic effect.

15. Antithesis

This is a contradiction that pits two ideas against each other in a balanced way. “You’re easy on the eyes, hard on the heart” is a line from a country song that illustrates this perfectly. This is often used to indicate just how something can be more than one thing at the same time.

16. Euphemism

Words that are used to soften the message are often considered euphemisms. “Passed away” is often used in place of “died” or “killed.” A “misunderstanding” might be used in place of “fight” or “argument.” And who could forget “wardrobe malfunction,” which is a fancy way of saying “your clothes fell off.”

17. Oxymoron

This puts two words together that seem to contradict each other. “Military intelligence,” “real phony,” “civil war,” and “silent yell” are all examples of an oxymoron. Many people use these to promote the humor in a situation.

Last edited by Jai Ganesh (2015-11-16 01:12:51)

Agnishom · 2015-11-08 00:14:09

Paradox is not a figure of speech, it is a philosophical problem where both P and not P seems true

Jai Ganesh · 2015-11-08 01:54:14

#10. A paradox is a figure of speech that appears to contradict itself. Examples of a paradox is I always lie or you can save money by spending it.

Paradox (literature)

This article is about the figure of speech.

In literature, the paradox is an anomalous juxtaposition of incongruous ideas for the sake of striking exposition or unexpected insight. It functions as a method of literary composition - and analysis - which involves examining apparently contradictory statements and drawing conclusions either to reconcile them or to explain their presence.

Literary or rhetorical paradoxes abound in the works of Oscar Wilde and G. K. Chesterton. Most literature deals with paradox of situation; Rabelais, Cervantes, Sterne, Borges, and Chesterton are recognized as masters of situation as well as verbal paradox. Statements such as Wilde’s “I can resist anything except temptation” and Chesterton’s “spies do not look like spies” are examples of rhetorical paradox. Further back, Polonius’ observation that “though this be madness, yet there is method in’t” is a memorable third. Also, statements that are illogical and metaphoric may be called "paradoxes", for example "the pike flew to the tree to sing". The literal meaning is illogical, but there are many interpretations for this metaphor.

Jai Ganesh · 2015-11-08 22:53:14

The Fields Medal is a prize awarded to two, three, or four mathematicians under 40 years of age at the International Congress of the International Mathematical Union (IMU), a meeting that takes place every four years. The Fields Medal is sometimes viewed as the highest honour a mathematician can receive. The Fields Medal and the Abel Prize have often been described as the "mathematician's Nobel Prize" (but different at least for the age restriction).

The prize comes with a monetary award, which since 2006 has been C$15,000 (in Canadian dollars). The colloquial name is in honour of Canadian mathematician John Charles Fields. Fields was instrumental in establishing the award, designing the medal itself, and funding the monetary component.

The medal was first awarded in 1936 to Finnish mathematician Lars Ahlfors and American mathematician Jesse Douglas, and it has been awarded every four years since 1950. Its purpose is to give recognition and support to younger mathematical researchers who have made major contributions.

In 2014 Maryam Mirzakhani became the first woman as well as the first Iranian, and Artur Avila became the first mathematician from Latin America to be awarded a Fields Medal.

The Fields Medal is awarded every four years during the opening ceremony of the International Congress of Mathematicians (ICM). It recognizes outstanding mathematical achievement for existing work and for the promise of future achievement. Two to four medals are awarded to mathematicians who have to be of age less than forty years on January 1 of the Congress year. The Fields Medal, established in 1936 and named after the Canadian mathematician J. C. Fields, is one of the most prestigious awards in the field of mathematics and often described as the “Nobel Prize of Mathematics”.

Last edited by Jai Ganesh (2015-11-08 23:35:33)

Jai Ganesh · 2015-11-09 17:57:10

The Challenger Deep is the deepest known point in the Earth's seabed hydrosphere, with a depth of 10,898 to 10,916 m (35,755 to 35,814 ft) by direct measurement from submersibles, and slightly more by sonar bathymetry (see below). It is in the Pacific Ocean, at the southern end of the Mariana Trench near the Mariana Islands group. The Challenger Deep is a relatively small slot-shaped depression in the bottom of a considerably larger crescent-shaped oceanic trench, which itself is an unusually deep feature in the ocean floor. Its bottom is about 11 km (7 mi) long and 1.6 km (1 mi) wide, with gently sloping sides. The closest land to the Challenger Deep is Fais Island (one of the outer islands of Yap), 287 km (178 mi) southwest, and Guam, 304 km (189 mi) to the northeast. It is located in the ocean territory of the Federated States of Micronesia, 1.6 km (1 mi) from its border with ocean territory associated with Guam.

The depression is named after the British Royal Navy survey ship HMS Challenger, whose expedition of 1872–1876 made the first recordings of its depth. According to the August 2011 version of the GEBCO Gazetteer of Undersea Feature Names, the location and depth of the Challenger Deep are 11°22.4′N 142°35.5′E and 10,920 m (35,827 ft) ±10 m (33 ft).

Jai Ganesh · 2015-11-11 01:38:17

Nadia Comaneci

Birth Date
November 12, 1961 (age 54)

Place of Birth
Gheorghe Gheorghiu-Dej, Romania

AKA
Nadia Comaneci
Full Name
Nadia Elena Comaneci

Nadia Comaneci is a Romanian gymnast who became the first woman to score a perfect 10 in an Olympic gymnastics event in 1976, at age 14.

quotes
“Hard work has made it easy. That is my secret. That is why I win.”
—Nadia Comaneci

Born in 1961, Romanian gymnast Nadia Comaneci became the first woman to score a perfect 10 in an Olympic gymnastics event at the 1976 Olympic Games, at age 14. Her performance at the 1976 Olympics redefined both her sport and audiences' expectations of female athletes. At the 1980 Olympics, Comaneci won gold medals for the balance beam and floor exercise. She retired from competition in 1984 and defected to the United States in 1989.

Early Life and Career

Nadia Elena Comaneci was born on November 12, 1961, in Gheorghe Gheorghiu-Dej, Romania, in the Carpathian Mountains, to parents Alexandria and Gheorghe, an auto mechanic. Comaneci was discovered at the age of 6 by gymnastics coach Bela Karolyi (later to become the Romanian national coach). She won the Romanian National Junior Championships, and, as a senior, won the European Championships in 1975 and the American Cup in 1976.

1976 Olympic Games

Comaneci thrilled the world at the 1976 Olympic Games in Montreal, Canada, where, at the age of 14, she became the first woman to score a perfect 10 in an Olympic gymnastics event. She received seven perfect scores and won three gold medals—for the uneven bars, balance beam and individual all-around—together with a bronze medal as part of the second-place Romanian national team. Comaneci's performance at the 1976 Olympics redefined both her sport and audiences' expectations of female athletes.

1980 Olympics and Later Years

At the 1980 Olympic Games in Moscow, Russia, Nadia Comaneci won two gold, for the balance beam and floor exercise (in which she tied with Soviet gymnast Nellie Kim); and two silver medals, for the team competition and individual all-around. (After coaching the Romanian national team through two Olympiads, Bela Karolyi defected to the United States in 1981. He later led the nation's gymnastic program to its first World Championships.)

Comaneci retired from competition in 1984 and worked as a coach for the Romanian team before defecting to the United States via Hungary in 1989. After appearing in a series of provocative underwear advertisements, she married American gymnast Bart Conner in 1996 and moved to Norman, Oklahoma.

In 1999, Comaneci received a World Sports Award of the Century after being elected "Athlete of the Century" during a gala in Vienna, Austria.

Comaneci currently does television commentary and writes for gymnastic publications.

Last edited by Jai Ganesh (2015-12-10 18:32:40)

Jai Ganesh · 2015-11-11 09:57:53

Stephen William Hawking CH, CBE, FRS, FRSA (born 8 January 1942) is an English theoretical physicist, cosmologist, author and Director of Research at the Centre for Theoretical Cosmology within the University of Cambridge. His scientific works include a collaboration with Roger Penrose on gravitational singularity theorems in the framework of general relativity, and the theoretical prediction that black holes emit radiation, often called Hawking radiation. Hawking was the first to set forth a theory of cosmology explained by a union of the general theory of relativity and quantum mechanics. He is a vigorous supporter of the many-worlds interpretation of quantum mechanics.

He is an Honorary Fellow of the Royal Society of Arts, a lifetime member of the Pontifical Academy of Sciences, and a recipient of the Presidential Medal of Freedom, the highest civilian award in the United States. Hawking was the Lucasian Professor of Mathematics at the University of Cambridge between 1979 and 2009 and has achieved commercial success with works of popular science in which he discusses his own theories and cosmology in general; his book 'A Brief History of Time' appeared on the British Sunday Times best-seller list for a record-breaking 237 weeks.

Hawking suffers from a rare early-onset, slow-progressing form of amyotrophic lateral sclerosis (ALS), also known as motor neurone disease or Lou Gehrig's disease, that has gradually paralysed him over the decades. He now communicates using a single cheek muscle attached to a speech-generating device. Hawking married twice and has three children.

Known for :

Hawking radiation
Penrose–Hawking theorems
A Brief History of Time (1988)

Notable awards :

Adams Prize (1966)
FRS (1974)
Eddington Medal (1975)
Maxwell Medal and Prize (1976)
Heineman Prize (1976)
Hughes Medal (1976)
Albert Einstein Award (1978)
CBE (1982)
RAS Gold Medal (1985)
Dirac Medal (1987)
Wolf Prize (1988)
CH (1989)
Prince of Asturias Award (1989)
Andrew Gemant Award (1998)
Naylor Prize and Lectureship (1999)
Lilienfeld Prize (1999)
Albert Medal (Royal Society of Arts) (1999)
Copley Medal (2006)
Presidential Medal of Freedom (2009)
Fundamental Physics Prize (2012)

Hawking has received numerous awards and honours. Already early in the list, in 1974 he was elected a Fellow of the Royal Society (FRS). At that time, his nomination read:

"Hawking has made major contributions to the field of general relativity. These derive from a deep understanding of what is relevant to physics and astronomy, and especially from a mastery of wholly new mathematical techniques. Following the pioneering work of Penrose he established, partly alone and partly in collaboration with Penrose, a series of successively stronger theorems establishing the fundamental result that all realistic cosmological models must possess singularities. Using similar techniques, Hawking has proved the basic theorems on the laws governing black holes: that stationary solutions of Einstein's equations with smooth event horizons must necessarily be axisymmetric; and that in the evolution and interaction of black holes, the total surface area of the event horizons must increase. In collaboration with G. Ellis, Hawking is the author of an impressive and original treatise on "Space-time in the Large".

The citation continues:

"Other important work by Hawking relates to the interpretation of cosmological observations and to the design of gravitational wave detectors".

Quotes :

On Quiet People - Quiet people have the loudest minds.

On Communication - For millions of years, mankind lived just like the animals. Then something happened which unleashed the power of our imagination. We learned to talk and we learned to listen. Speech has allowed the communication of ideas, enabling human beings to work together to build the impossible. Mankind’s greatest achievements have come about by talking, and its greatest failures by not talking. It doesn’t have to be like this. Our greatest hopes could become reality in the future. With the technology at our disposal, the possibilities are unbounded. All we need to do is make sure we keep talking.

On Intelligence - Intelligence is the ability to adapt to change.

On Being Curious - It surprises me how disinterested we are today about things like physics, space, the universe and philosophy of our existence, our purpose, our final destination. It’s a crazy world out there. Be curious.”

On Understanding The Universe - My goal is simple. It is a complete understanding of the universe, why it is as it is and why it exists at all.

On The Difference Between Religion and Science - There is a fundamental difference between religion, which is based on authority, and science, which is based on observation and reason. Science will win because it works.

On Being Free - Although I cannot move and I have to speak through a computer, in my mind I am free.

On Destiny - I have noticed that even those who assert that everything is predestined and that we can change nothing about it still look both ways before they cross the street.

On Perfection - One of the basic rules of the universe is that nothing is perfect. Perfection simply doesn’t exist…..Without imperfection, neither you nor I would exist.

On The Downside Of Being A Celebrity - The downside of my celebrity is that I cannot go anywhere in the world without being recognized. It is not enough for me to wear dark sunglasses and a wig. The wheelchair gives me away.

On Death - I’m not afraid of death, but I’m in no hurry to die.

On Aliens - If aliens ever visit us, I think the outcome would be much as when Christopher Columbus first landed in America, which didn’t turn out very well for the Native Americans.

On Reading - Nothing is better than reading and gaining more and more knowledge.

About the Legacy Project

The Legacy Project is an initiative that hopes to inspire you through providing you with unlimited access to extraordinary individuals, each of whom have achieved Greatness in their own, unique and varying form. Each person who we interview and profile provides you with a different viewpoint, as well as different lessons to learn from.

Jai Ganesh · 2015-11-12 01:25:37

A light-year (abbreviation: ly), sometimes written light year, is a unit of length used informally to express astronomical distances. It is approximately 9 trillion kilometres (or about 6 trillion miles). As defined by the International Astronomical Union (IAU), a light-year is the distance that light travels in vacuum in one Julian year. Because it includes the word year, the term light-year is sometimes misinterpreted as a unit of time.

The light-year is most often used when expressing distances to stars and other distances on a galactic scale, especially in non-specialist and popular science publications. The unit usually used in professional astrometry is the parsec (symbol: pc, approximately 3.26 light-years; the distance at which one astronomical unit subtends an angle of one second of arc).

The light-year unit appeared a few years after the first successful measurement of the distance to a star other than our Sun, by Friedrich Bessel in 1838. The star was 61 Cygni, and he used a 6.2-inch (160 mm) heliometer designed by Joseph von Fraunhofer. The largest unit for expressing distances across space at that time was the astronomical unit, equal to the radius of the Earth's orbit (

km or mi). In those terms, trigonometric calculations based on 61 Cygni's parallax of 0.314 arcseconds, showed the distance to the star to be 660000 astronomical units ( km or mi). Bessel added that light employs 10.3 years to traverse this distance. He recognized that his readers would enjoy the mental picture of the approximate transit time for light, but he refrained from using the light-year as a unit. He may have resented expressing distances in light-years because it would deteriorate the accuracy of his parallax data due to multiplying with the uncertain parameter of the speed of light. The speed of light was not yet precisely known in 1838; its value changed in 1849 (Fizeau) and 1862 (Foucault). It was not yet considered to be a fundamental constant of nature, and the propagation of light through the aether or space was still enigmatic. The light-year unit appeared, however, in 1851 in a German popular astronomical article by Otto Ule. The paradox of a distance unit name ending on year was explained by Ule by comparing it to a hiking road hour (Wegstunde). A contemporary German popular astronomical book also noticed that light-year is an odd name. In 1868 an English journal labelled the light-year as a unit used by the Germans. Eddington called the light-year an inconvenvient and irrelevant unit, which had sometimes crept from popular use into technical investigations.

Although modern astronomers often prefer to use the parsec, light years are also popularly used to gauge the expanses of interstellar and intergalactic space.

Usage of term

Distances expressed in light-years include those between stars in the same general area, such as those belonging to the same spiral arm or globular cluster. Galaxies themselves span from a few thousand to a few hundred thousand light-years in diameter, and are separated from neighbouring galaxies and galaxy clusters by millions of light-years. Distances to objects such as quasars and the Sloan Great Wall run up into the billions of light-years.

Agnishom · 2015-11-21 00:46:52

Agnishom wrote:

bobbym wrote:
The title means cream of the cream. Translates into the best of the best.
What do I need to accomplish to make it to this list?

bobbym · 2015-11-21 07:18:45

Agnishom wrote:

What do I need to accomplish to make it to this list?

If you are asking me then I would say you should ask this question in your own new thread, then I would attempt to answer there. I try to keep comments that are not germane to a thread to a minimum.

Math Is Fun Forum

#1 2015-10-25 12:27:50

crème de la crème

#2 2015-10-25 17:58:53

Re: crème de la crème

#3 2015-10-25 20:19:32

Re: crème de la crème

#4 2015-10-27 09:16:16

Re: crème de la crème

#5 2015-11-02 16:50:23

Re: crème de la crème

#6 2015-11-03 02:52:29

Re: crème de la crème

#7 2015-11-03 04:41:58

Re: crème de la crème

#8 2015-11-03 06:23:50

Re: crème de la crème

#9 2015-11-03 08:29:28

Re: crème de la crème

#10 2015-11-03 17:40:14

Re: crème de la crème

#11 2015-11-04 01:55:41

Re: crème de la crème

#12 2015-11-04 04:15:44

Re: crème de la crème

#13 2015-11-05 11:42:23

Re: crème de la crème

#14 2015-11-05 14:56:22

Re: crème de la crème

#15 2015-11-07 00:19:20

Re: crème de la crème

#16 2015-11-07 12:43:37

Re: crème de la crème

#17 2015-11-08 00:14:09

Re: crème de la crème

#18 2015-11-08 01:54:14

Re: crème de la crème

#19 2015-11-08 22:53:14

Re: crème de la crème

#20 2015-11-09 17:57:10

Re: crème de la crème

#21 2015-11-11 01:38:17

Re: crème de la crème

#22 2015-11-11 09:57:53

Re: crème de la crème

#23 2015-11-12 01:25:37

Re: crème de la crème

#24 2015-11-21 00:46:52

Re: crème de la crème

#25 2015-11-21 07:18:45

Re: crème de la crème

Board footer